Mesurer l’impact des vidéos d’influenceurs (par exemple) sur YouTube reste un exercice complexe. Il est tentant d’imaginer qu’une vidéo qui accumule des vues, des likes et des commentaires puisse mécaniquement entraîner une hausse des réservations touristiques dans une destination.
Mais établir une relation de cause à effet entre visibilité en ligne et comportements de consommation réels — comme le choix d’une destination de vacances — relève davantage du fantasme que d’une corrélation vérifiable.
Ici, à partir d’un simple mot-clé, il est possible d’explorer la structure d’un réseau de vidéos YouTube : celles-ci peuvent être reliées par contenu similaire, communautés de public, profils de performance ou clustering.
Il y a donc 4 approches complémentaires et relativement “innovantes”.
La première approche s’intéresse aux commentateurs communs. Deux vidéos sont connectées si elles partagent des commentateurs ayant laissé des commentaires sur les deux contenus.
Ce réseau social n’analyse pas les contenus eux-mêmes, mais “cartographie les circulations d’audience”.
La seconde approche s’appuie sur la similarité sémantique : elle relie les vidéos en fonction de la proximité de leur titre, description (et tags, si disponibles).
Les textes sont transformés en vecteurs grâce à un modèle d’embedding “léger” (basé sur un modèle pré-entraîné de type LLM), mais suffisant. Les liens entre vidéos sont ensuite mesurés par similarité cosinus.
Une troisième méthode consiste à construire un réseau à partir des métriques de performance (nombre de vues, de likes et de commentaires). Chaque vidéo est représentée par un vecteur, et les liens sont établis selon la similarité cosinus entre ces vecteurs.
Plus classique, cette approche permet d’identifier des regroupements de vidéos aux trajectoires similaires en termes de visibilité.
Une quatrième méthode, qui n’utilise pas la théorie des graphes, repose sur l’algorithme K-Means. Elle permet de regrouper les vidéos en clusters selon leurs métriques numériques (vues, likes, commentaires). »
1. Définition du mot-clé et extraction des vidéos
Avant toute chose, vous devez saisir un mot-clé (ou plusieurs, séparés par des virgules) dans l’interface.
Ce ou ces mots-clés serviront à interroger l’API YouTube Data v3 pour récupérer les vidéos correspondantes.
Ensuite, vous devez indiquer le nombre de vidéos à extraire à partir de ces termes. Il est fortement recommandé de commencer par un volume réduit (par exemple, 100 vidéos) afin de tester le bon fonctionnement du script. Le système est conçu pour permettre l’analyse jusqu’à 1000 vidéos, grâce à une boucle qui enchaîne les requêtes de manière optimisée.
Toutefois, gardez à l’esprit que cette opération consomme rapidement votre quota de requêtes API fourni par Google.
2. Réseau par commentaires communs
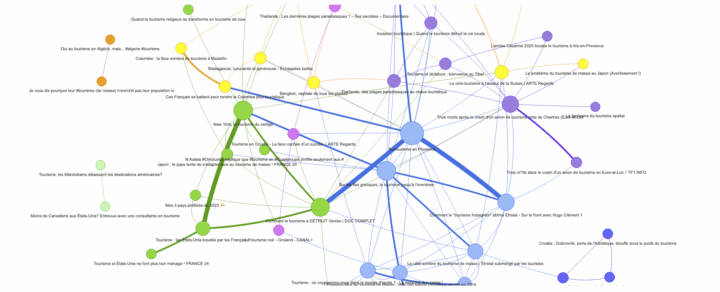
L’indicateur commentaires communs mesure le degré de lien social entre deux vidéos YouTube. Il s’appuie sur le fait que certains utilisateurs commentent plusieurs vidéos différentes. Lorsque deux vidéos partagent un ou plusieurs commentateurs, cela suggère une proximité thématique, d’audience ou de circulation des contenus.
Dans le graphe, chaque lien (arêtes du graphe) entre deux vidéos est pondéré par le nombre de commentateurs communs qu’elles partagent. Plus ce nombre est élevé, plus les vidéos sont considérées comme connectées socialement.
Le réseau construit à partir des commentateurs communs repose donc sur une logique sociale : deux vidéos sont reliées entre elles si des internautes ont commenté les deux contenus. Le script analyse donc les commentaires. Vous pouvez définir dans l’interface le nombre de commentaires “max” à analyser par vidéo.
Ce type de graphe est utile pour analyser la circulation sociale des contenus, autour de thématiques (mots clés).
B = nx.Graph()
for vid in video_ids:
B.add_node(vid, bipartite=0)
try:
rep = yt.commentThreads().list(
part="snippet", videoId=vid, maxResults=nb_commentaires, textFormat="plainText"
).execute()
for item in rep.get("items", []):
snip = item["snippet"]["topLevelComment"]["snippet"]
auteur = snip.get("authorChannelId", {}).get("value")
if auteur:
B.add_node(auteur, bipartite=1)
B.add_edge(vid, auteur)
except:
continue
videos = [n for n, d in B.nodes(data=True) if d["bipartite"] == 0]
G = bipartite.weighted_projected_graph(B, videos)
for u, v, d in G.edges(data=True):
if d["weight"] >= seuil_co:
G2.add_edge(u, v, weight=d["weight"])
Cette partie du code construit un graphe biparti vidéo ↔ commentateur, puis projette ce graphe uniquement sur les vidéos, en gardant comme poids le nombre de commentateurs communs.
3. Réseau par similarité sémantique
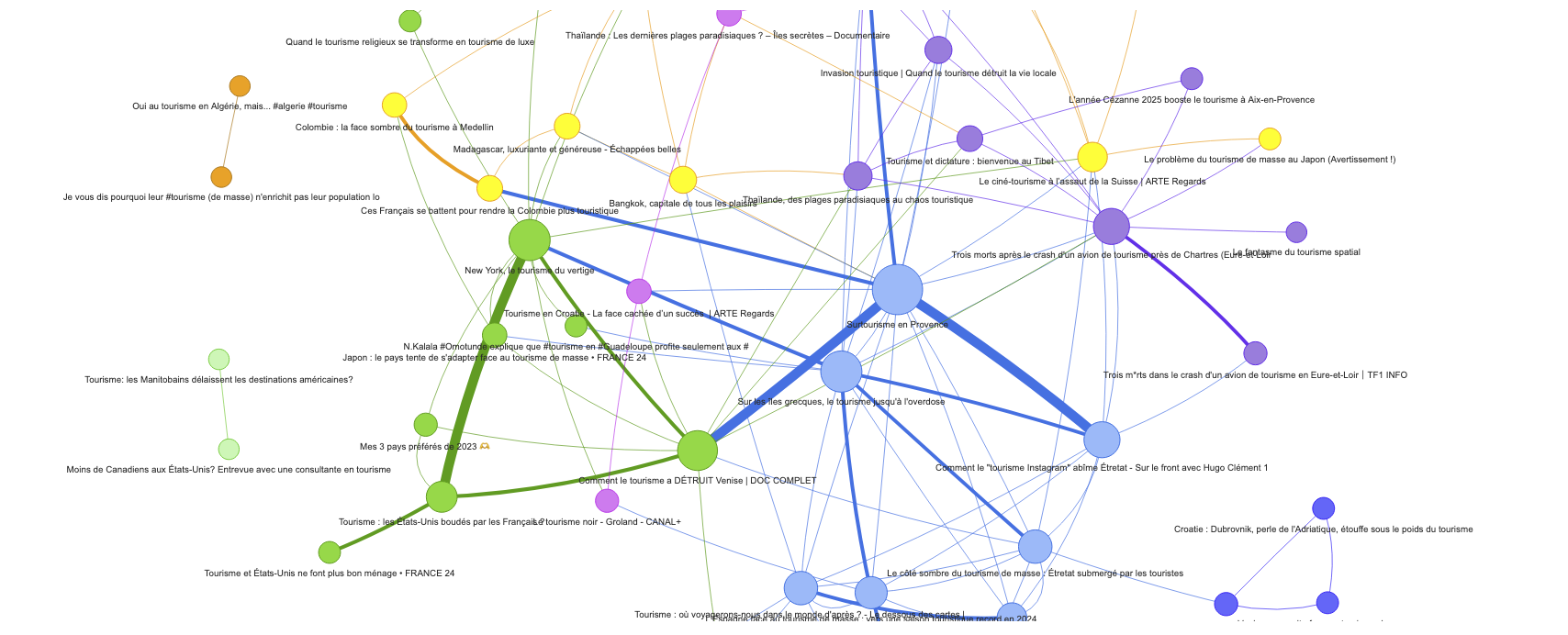
Le réseau sémantique relie les vidéos en fonction de la proximité lexicale de leurs contenus éditoriaux.
Pour cela, chaque vidéo est décrite à partir de son titre, sa description (et ses tags, si disponibles). Ces textes sont transformés en vecteurs via un modèle de langage léger, basé sur la bibliothèque sentence-transformers (modèle : paraphrase-multilingual-MiniLM-L12-v2), qui produit des embeddings : des représentations denses et contextualisées du contenu.
Deux vidéos sont connectées dans le réseau si la similarité cosinus entre leurs vecteurs dépasse un seuil défini.
Ce seuil se définit dans l’interface Streamlit.
Ce graphe révèle des proximités thématiques, indépendamment des interactions sociales.
from sentence_transformers import SentenceTransformer, util
model = SentenceTransformer('multilingual-MiniLM-L12-v2')
textes = [titres[v] + " " + descriptions[v] for v in video_ids]
embeddings = model.encode(textes, convert_to_tensor=True)
sim = util.cos_sim(embeddings, embeddings)
for i in range(len(video_ids)):
for j in range(i + 1, len(video_ids)):
score = sim[i][j].item()
if score >= seuil_sim:
G2.add_edge(video_ids[i], video_ids[j], weight=score)
Ce code applique donc un modèle de langage par embeddings, “multilingual-MiniLM-L12-v2″, sur le titre + description de chaque vidéo, puis mesure la similarité cosinus entre les paires de vidéos. Si la similarité dépasse un seuil défini par l’utilisateur (seuil_sim), une arête est ajoutée entre les deux vidéos.
4. Réseau par métriques numériques
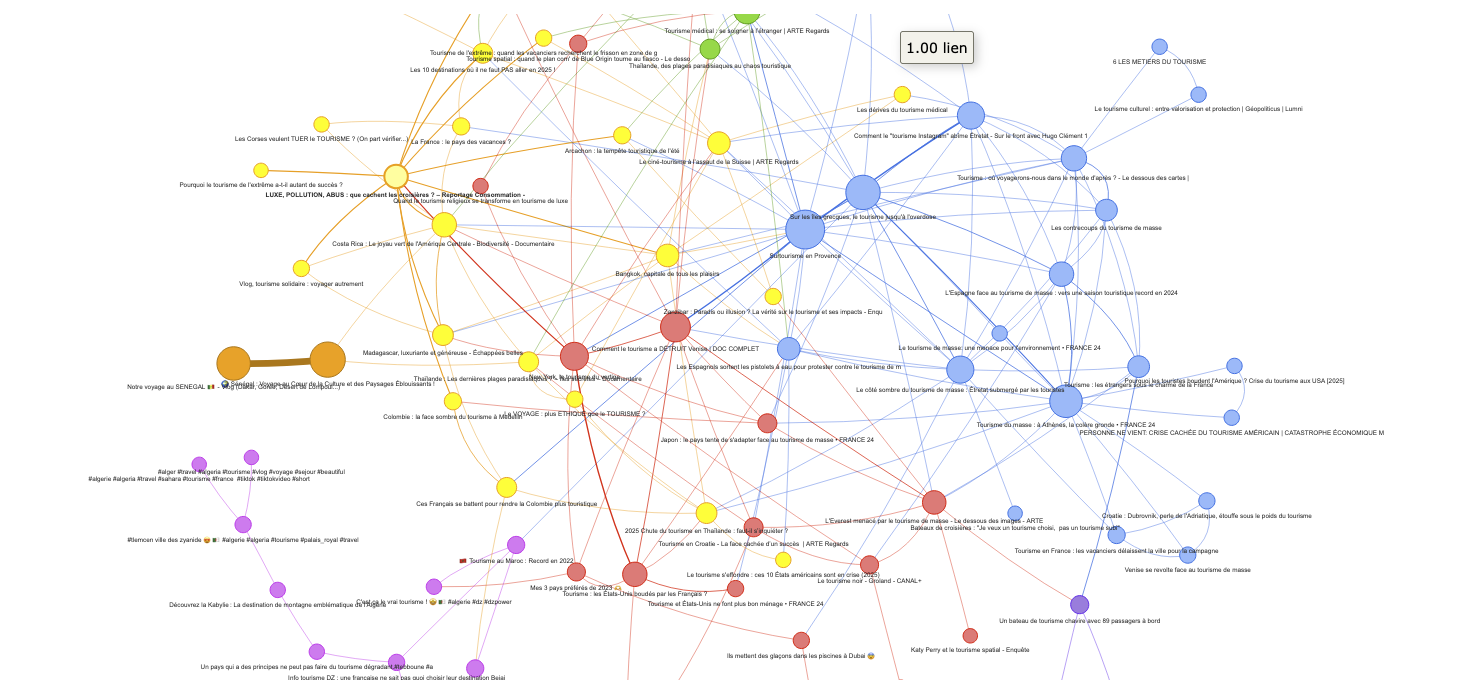
Le réseau métrique repose sur des indicateurs de performance : nombre de vues, de likes, et de commentaires pour chaque vidéo. Ces trois dimensions sont combinées en un vecteur pour chaque contenu, puis comparées via une similarité cosinus.
Deux vidéos sont reliées si leur audience est similaire, ce qui permet de cartographier les contenus à succès comparables, toutes thématiques confondues.
Ce type d’analyse est utile pour étudier les effets de viralité, ou pour identifier des profils typiques de vidéo performante dans un groupe/thème.
X = [[vues_d[v], likes_d[v], comments_d[v]] for v in video_ids]
X_scaled = MinMaxScaler().fit_transform(X)
sim = cosine_similarity(X_scaled)
for i in range(len(video_ids)):
for j in range(i + 1, len(video_ids)):
score = sim[i][j]
if score >= seuil_sim:
G2.add_edge(video_ids[i], video_ids[j], weight=score)
Chaque vidéo est représentée par un vecteur [vues, likes, commentaires], normalisé avec MinMaxScaler, puis comparé à tous les autres via similarité cosinus. Cela permet donc de relier des vidéos qui ont des profils de performance similaires.
Le réseau construit à partir des métriques permet non seulement de regrouper les vidéos très populaires, mais aussi d’identifier des ensembles de vidéos moins visibles qui partagent des caractéristiques similaires.
Cette approche offre un moyen d’explorer la “longue traîne” (en référence à la longue traîne en SEO) des contenus YouTube, révélant des dynamiques d’intérêt souvent négligées mais potentiellement significatives.
4.1 Comment cela fonctionne ?
Exemple à partir de trois vidéos :
A = [12000, 800, 150] #vues #likes #commentaires B = [100000, 3000, 450] #vues #likes #commentaires C = [11500, 900, 130] #vues #likes #commentaires
Mais ces valeurs ne sont pas comparables directement : les vues ont des ordres de grandeur bien plus grands que les commentaires.
4.2 Étape de normalisation des données
On applique une normalisation “Min-Max” avec MinMaxScaler() pour amener toutes les dimensions entre 0 et 1 :
A = [0.01, 0.0, 0.05] B = [1.0, 1.0, 1.0] C = [0.0, 0.05, 0.0]
Cela évite que les vues (plus grandes) écrasent les autres métriques dans le calcul de similarité.
4.3 Calcul de la similarité cosinus
On utilise la similarité cosinus pour mesurer à quel point deux vecteurs sont “similaires”, c’est-à-dire si deux vidéos ont des profils métriques similaires.
from sklearn.metrics.pairwise import cosine_similarity similarites = cosine_similarity(X_scaled)
6. Clustering K-Means sur les métriques des vidéos YouTube
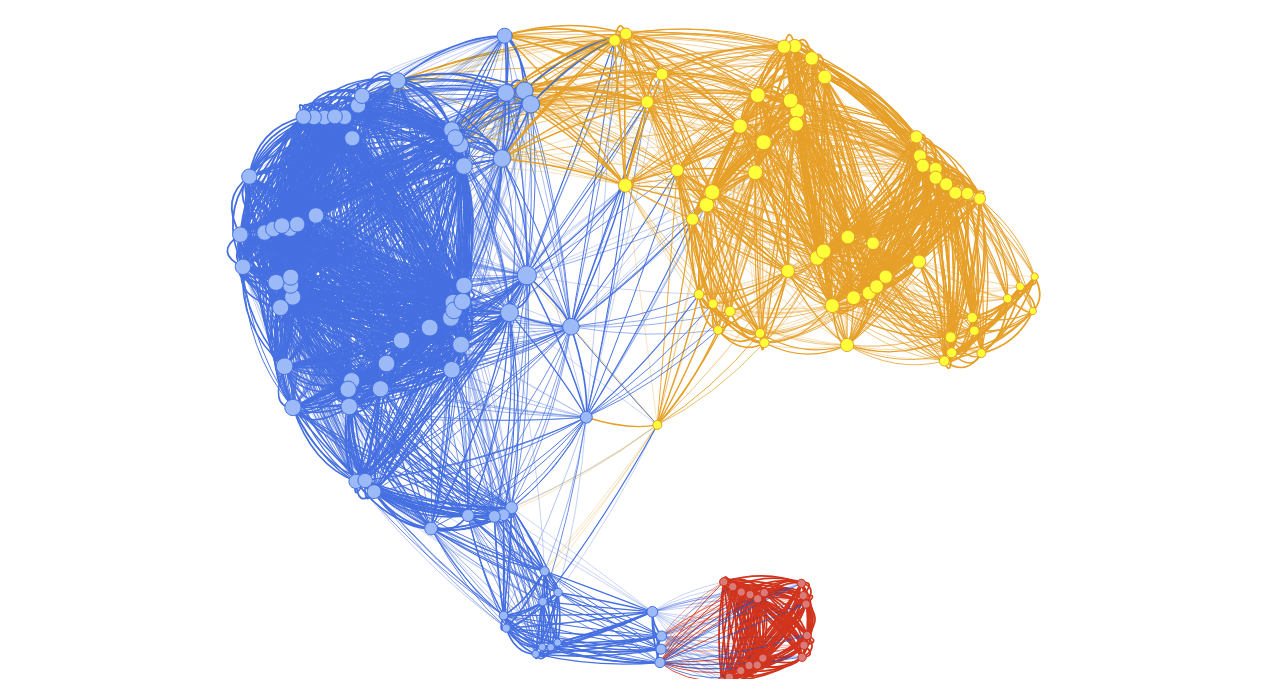
L’analyse par K-Means appliquée aux métriques (vues, likes, commentaires) permet de regrouper automatiquement les vidéos selon leur profil d’engagement. Contrairement aux approches basées sur la similarité cosinus, qui mesurent les proximités entre paires de vidéos, le clustering identifie des groupes cohérents dans l’ensemble des vidéos, sans hypothèse préalable sur les relations. Après normalisation des données pour rendre comparables les différentes échelles, l’algorithme K-Means partitionne les vidéos en un nombre de clusters défini (ou estimé) automatiquement.
K-Means est un algorithme de classification non supervisée qui regroupe des données en k clusters (groupes) en se basant sur leur proximité. Chaque cluster est représenté par un centre de gravité appelé centroïde.
Le fonctionnement repose sur un processus itératif : à partir de k centroïdes initialisés (aléatoirement), l’algorithme affecte chaque point au centroïde le plus proche, puis recalcule les centroïdes en fonction des points qui leur sont assignés. Ce processus se répète jusqu’à une convergence “optimale”.
Pour déterminer le nombre optimal de clusters (k), on utilise souvent la méthode du coude : on trace la courbe de l’inertie intra-cluster (somme des distances entre les points et leur centroïde) en fonction de k. Le point où cette courbe commence à se stabiliser (forme un “coude”) indique un bon compromis entre complexité et qualité du regroupement.

Chaque cluster reflète un type de popularité : on peut ainsi repérer, par exemple, des vidéos très virales mais peu commentées, ou à l’inverse, des vidéos avec peu de vues mais un fort taux d’interaction.

