Propriétés des données textuelles – La loi de Zipf

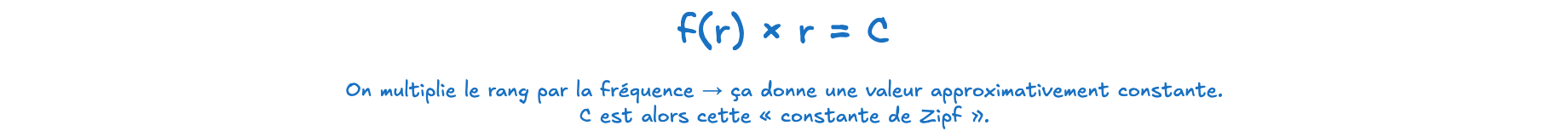
La loi de Zipf n’est pas à connaître dans le détail de ses formules, mais elle constitue la base de la compréhension de la structuration des données textuelles. De nombreux logiciels statistiques la calculent automatiquement comme première description d’un corpus.

Quand on commence à analyser un corpus de texte (entretiens clinique, articles de presse, tweets,..), on est souvent frappé par certains mots qui apparaissent très souvent.
Cette distribution n’est pas aléatoire : elle suit un principe mathématique appelé loi de Zipf. Cette loi se retrouve dans toutes les langues et tous les types de textes.
Elle révèle deux points importants qui conditionnent tout travail d’analyse textuelle :

Les mots fréquents sont souvent des “mots vides” (stopwords) : D’après la loi de  Zipf, quelques mots (mots outils) occupent les tout premiers rangs et apparaissent de très nombreuses fois dans un texte.
En français, ce sont souvent des déterminants (le, la, les, un, une, des…), des prépositions (à, de, en, sur…), ou des pronoms (il, elle, nous)…
Si on ne réalise pas de prétraitement, l’analyse risque d’être dominée par ces mots qui n’ont que peu d’intérêt sémantique.

La loi de Zipf met aussi en lumière les hapax : À l’autre extrémité du classement, on trouve une multitude de mots qui n’apparaissent qu’une seule fois dans tout le corpus.
Ces mots sont appelés des hapax (du grec “hapax legomenon” = “dit une seule fois”). Ils sont intéressants car ils introduisent de la richesse lexicale.

 

1. Qu’est-ce que la loi de Zipf ?

La loi de Zipf, formulée par le linguiste américain George Zipf, indique que : La fréquence d’un mot est inversement proportionnelle à son rang.

Attention, le rang ne correspond pas à l’ordre d’apparition du mot dans une phrase, mais à son classement en fonction de sa fréquence.

Prenons  comme exemple ces 5 phrases :

1. Le musée est au centre de la ville et il attire des visiteurs.
2. La vieille place est près de la rivière et la cathédrale domine la vue.
3. En été la ville organise des festivals et la musique résonne dans les rues.
4. Le marché local propose des produits frais et des spécialités régionales.
5. Le tourisme durable encourage les transports doux et la découverte lente.

Fréquences et rangs :

1. Rang 1 : « la » → 8
2. Rang 2 : « et » → 5
3. Rang 3 : « des » → 4
4. Rang 4 : « le » → 3
5. Rang 5 : « de », « est », « les », « ville » → 2 chacun

6. Rang 6 : tous les autres mots (fréquence = 1), dont « tourisme »…

 

2. Loi de Zipf : deux formulations

Une fois le principe compris, il n’est pas nécessaire de recourir aux formules : la simple observation de la courbe suffit le plus souvent à mettre en évidence la structure caractéristique décrite par la loi de Zipf.
Toutefois, afin d’étayer l’analyse, nous allons examiner les deux formulations de la loi de Zipf. Pour cela, nous simulons un corpus plus conséquent.
Après avoir comptabilisé les occurrences des mots, nous obtenons le classement suivant :

• Rang 1 : « le » → fréquence = 200
• Rang 2 : « de » → fréquence = 100
• Rang 3 : « la » → fréquence = 67
• Rang 10 : « pour » → fréquence = 20
• Rang 100 : « montagne » → fréquence = 2

2.1 Formulation 1 : proportion inverse

La loi de Zipf dit que la fréquence d’un mot est inversement proportionnelle à son rang :

 

3. Lire une courbe de Zipf

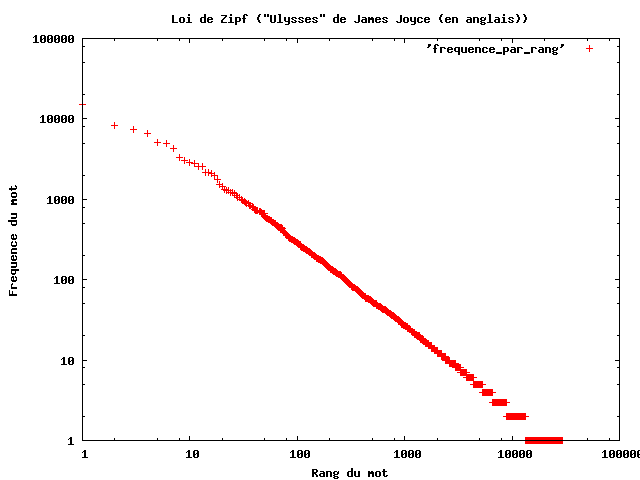
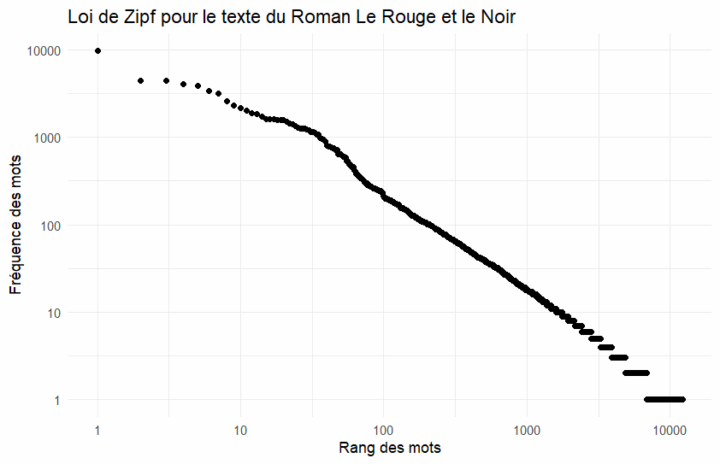
Quand on trace la loi de Zipf sur un graphique en échelle log-log :

• Axe des abscisses (x) = le rang du mot (1 pour le plus fréquent, 2 pour le suivant, etc.).
• Axe des ordonnées (y) = la fréquence du mot.
• On obtient une courbe qui descend rapidement à gauche (mots très fréquents) puis qui s’aplatit vers la droite (mots rares).

4. Le code source

Ce script permet d’importer un fichier texte afin d’examiner les propriétés statistiques du corpus à travers la loi de Zipf.
L’analyse est réalisée sur les données brutes, sans opération préalable de normalisation ou de nettoyage textuel.

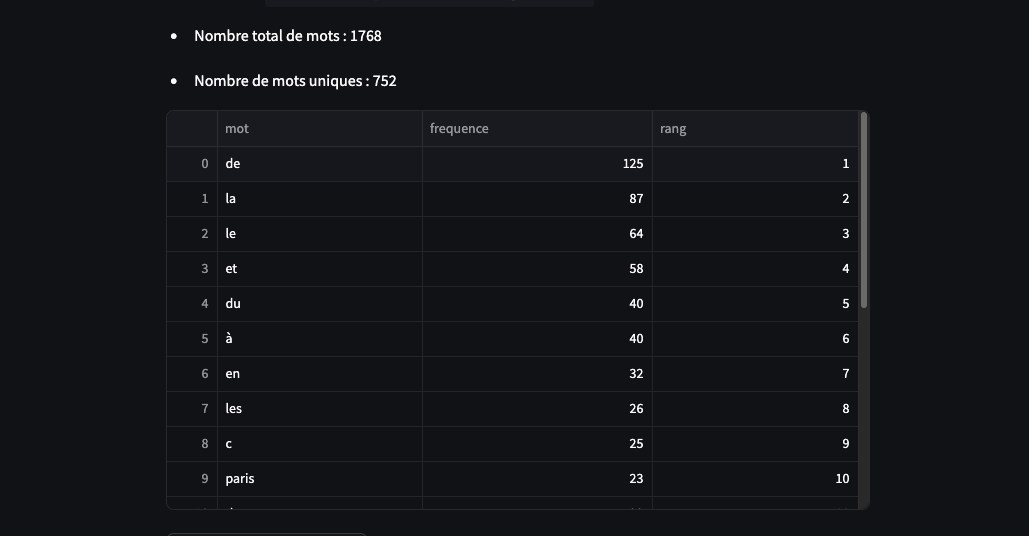
On retrouve bien la décroissance régulière : les premiers mots (“de”, “la”, “le”) ont une fréquence très élevée, puis la courbe chute rapidement.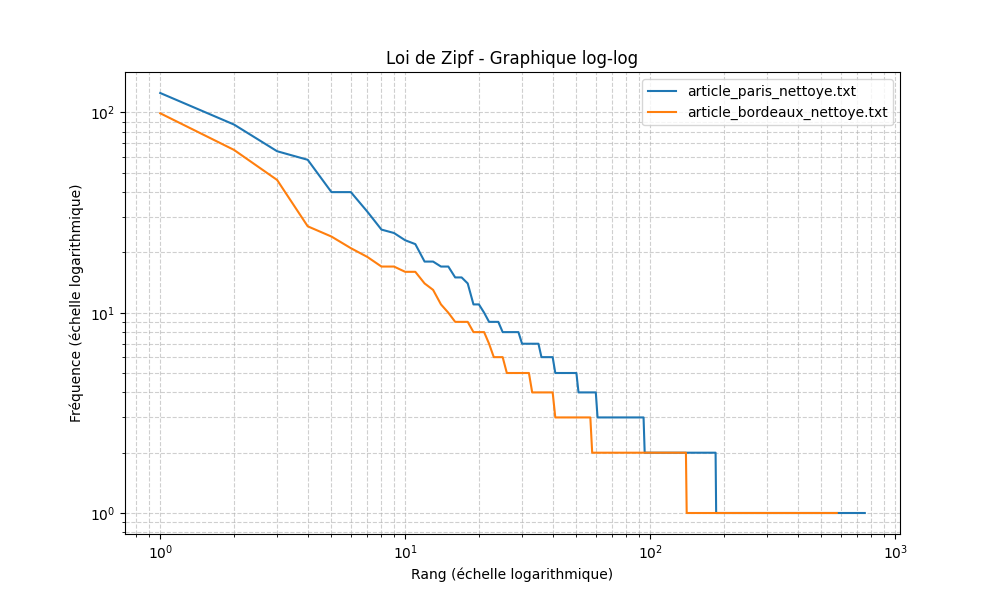

Le corpus utilisé dans cet exemple est trop restreint : même si la courbe rappelle la forme attendue par la loi de Zipf, elle présente des irrégularités liées à la petite taille de l’échantillon.

# pip install streamlit matplotlib pandas

import streamlit as st
import matplotlib.pyplot as plt
from collections import Counter
import pandas as pd
import io
import re

# Nettoyage et tokenisation
def nettoyer_et_tokeniser(texte):
    texte = texte.lower()
    texte = re.sub(r'[^\w\s]', '', texte)
    mots = texte.split()
    return mots

# Création de la matrice rang / fréquence
def analyser_zipf(mots):
    compteur = Counter(mots)
    data = pd.DataFrame(compteur.items(), columns=['mot', 'frequence'])
    data = data.sort_values(by='frequence', ascending=False).reset_index(drop=True)
    data['rang'] = data.index + 1
    return data

# Affichage de la courbe log-log
def tracer_zipf(dataframes, labels):
    plt.figure(figsize=(10, 6))
    for df, label in zip(dataframes, labels):
        plt.loglog(df['rang'], df['frequence'], label=label)
    plt.xlabel("Rang (échelle logarithmique)")
    plt.ylabel("Fréquence (échelle logarithmique)")
    plt.title("Loi de Zipf - Graphique log-log")
    plt.grid(True, which="both", linestyle="--", alpha=0.6)
    plt.legend()
    fig = plt.gcf()
    return fig

# Interface principale
st.title("Analyse textuelle – Loi de Zipf")

fichiers = st.file_uploader("Importer un ou plusieurs fichiers texte (.txt)", type="txt", accept_multiple_files=True)

if fichiers:
    st.divider()
    st.subheader("Résultats pour chaque fichier")

    dataframes = []
    noms_fichiers = []

    for fichier in fichiers:
        texte = fichier.read().decode('utf-8')
        mots = nettoyer_et_tokeniser(texte)
        df = analyser_zipf(mots)
        dataframes.append(df)
        noms_fichiers.append(fichier.name)

        st.markdown(f"### Fichier : `{fichier.name}`")
        st.write(f"- Nombre total de mots : {len(mots)}")
        st.write(f"- Nombre de mots uniques : {len(df)}")

        st.dataframe(df.head(20), use_container_width=True)

        # Export CSV
        csv_buffer = io.StringIO()
        df.to_csv(csv_buffer, index=False)
        st.download_button(
            label="Télécharger la matrice CSV",
            data=csv_buffer.getvalue(),
            file_name=f"{fichier.name}_zipf.csv",
            mime="text/csv"
        )

    st.divider()
    st.subheader("Graphique log-log de la loi de Zipf")

    fig = tracer_zipf(dataframes, noms_fichiers)
    st.pyplot(fig)

    # Export PNG
    image_buffer = io.BytesIO()
    fig.savefig(image_buffer, format='png')
    st.download_button(
        label="Télécharger le graphique",
        data=image_buffer.getvalue(),
        file_name="graphique_zipf.png",
        mime="image/png"
    )

    st.divider()
    st.subheader("Interprétation")

    st.markdown("""
La **loi de Zipf** est une observation statistique sur les mots d’un texte :  
Certains mots apparaissent très souvent, d’autres très rarement.

Dans le **graphique log-log** ci-dessus :

- L’**axe horizontal** représente le **rang** du mot : 1er mot le plus fréquent, 2e, 3e, etc.
- L’**axe vertical** représente le **nombre de fois que le mot apparaît**.

Les deux axes sont en **échelle logarithmique**.  
Cela signifie qu’au lieu d’augmenter régulièrement (1, 2, 3, 4...), ils progressent par puissances de 10 :  
**1 → 10 → 100 → 1000**, etc.

Pourquoi faire cela ?  
Parce que cela permet de mieux voir les différences **dans un très grand intervalle de valeurs**.  
Si tu affiches un mot très fréquent (comme "le", "de", "et") avec un mot très rare (comme "capitulaire", "mégajoule"),  
l’échelle normale serait illisible. Le **logarithme compresse visuellement les données** pour que la distribution soit observable.

---

### Pourquoi c’est important en NLP ?

- Cela montre que **seulement quelques mots dominent le texte**.
- Cela aide à comprendre que **supprimer ou pondérer ces mots** peut améliorer la qualité de la représentation.
- C’est aussi utile pour **trier les mots rares**, souvent synonymes d’information spécifique.
- C’est aussi utile pour **trier les mots trop fréquents**, souvent synonymes de bruit.
- En résumé, **la loi de Zipf aide à mieux modéliser le langage naturel**.

    """)

 

Conclusion

La loi de Zipf est une étape incontournable pour comprendre la distribution du vocabulaire dans un texte.
Ce que l’on doit retenir :

• La fréquence diminue vite quand le rang augmente.
• Le produit f(r) * r reste (normalement) approximativement constant
• Cela explique pourquoi, dans l’analyse de texte, il faut nettoyer les stopwords (qui dominent le haut du classement) et parfois examiner les hapax (rang très élevé, fréquence = 1).